Hierarchical Group Effects in seroCOP

Source: vignettes/hierarchical-groups.Rmd

Introduction

This vignette demonstrates how to use hierarchical modeling in SeroCOP to account for group-level heterogeneity in correlates of protection. This is particularly useful when different subpopulations (e.g., age groups, geographic regions, or vaccine types) may have different dose-response relationships.

When to Use Hierarchical Models

Hierarchical modeling is appropriate when:

  • You have multiple groups that may differ in their correlate of protection relationships
  • You want to “borrow strength” across groups while allowing group-specific estimates
  • You want to quantify between-group variability in protection
  • Sample sizes within groups may be modest

Example Scenario: Age-Specific Correlates

We’ll demonstrate with a realistic scenario where antibody titre is a correlate of protection, but the strength of this relationship varies by age group:

  • Young adults: Steep relationship (strong correlate)
  • Middle-aged: Moderate relationship
  • Older adults: Flat relationship (weak or no correlate)

This reflects real-world phenomena where immune responses may differ by age.

Load the package

Simulate Age-Stratified Data

We’ll create data for three age groups with different correlate of protection relationships:

n_per_group <- 80  # Sample size per age group

# Function to simulate data for one age group
simulate_group <- function(n, group_name, slope, ec50) {
  # Generate antibody titres
  titre <- rnorm(n, mean = 2.5, sd = 2.0)
  
  # Calculate infection probability using the logistic model
  # floor = 0.05, ceiling = 0.70
  floor <- 0.05
  ceiling <- 0.70
  
  logit_part <- 1 / (1 + exp(slope * (titre - ec50)))
  prob_infection <- ceiling * (logit_part * (1 - floor) + floor)
  
  # Generate infection outcomes
  infected <- rbinom(n, 1, prob_infection)
  
  return(data.frame(
    titre = titre,
    infected = infected,
    age_group = group_name
  ))
}

# Simulate three age groups with different CoP strengths
# Note: Higher slope values mean steeper curves (stronger correlate)
young <- simulate_group(n_per_group, "Young", slope = 3.0, ec50 = 1.5)
middle <- simulate_group(n_per_group, "Middle", slope = 1.5, ec50 = 1.8)
old <- simulate_group(n_per_group, "Old", slope = 0.3, ec50 = 2.0)

# Combine all groups
all_data <- rbind(young, middle, old)

cat(sprintf("Simulated data with age-specific correlates:\n"))
#> Simulated data with age-specific correlates:
cat(sprintf("  Young (n=%d): slope=3.0, ec50=1.5 (steep - strong protection)\n", n_per_group))
#>   Young (n=80): slope=3.0, ec50=1.5 (steep - strong protection)
cat(sprintf("  Middle (n=%d): slope=1.5, ec50=1.8 (moderate protection)\n", n_per_group))
#>   Middle (n=80): slope=1.5, ec50=1.8 (moderate protection)
cat(sprintf("  Old (n=%d): slope=0.3, ec50=2.0 (flat - weak correlate)\n", n_per_group))
#>   Old (n=80): slope=0.3, ec50=2.0 (flat - weak correlate)
cat(sprintf("\nTotal sample size: %d\n", nrow(all_data)))
#> 
#> Total sample size: 240
cat(sprintf("Overall infection rate: %.1f%%\n", 100 * mean(all_data$infected)))
#> Overall infection rate: 25.4%

Let’s visualize the raw data:

ggplot(all_data, aes(x = titre, y = infected, color = age_group)) +
  geom_point(alpha = 0.4, position = position_jitter(height = 0.02)) +
  geom_smooth(method = "loess", se = TRUE, linewidth = 1) +
  facet_wrap(~age_group) +
  labs(
    title = "Infection vs Titre by Age Group",
    x = "Antibody Titre (log scale)",
    y = "Infected (0/1)",
    color = "Age Group"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")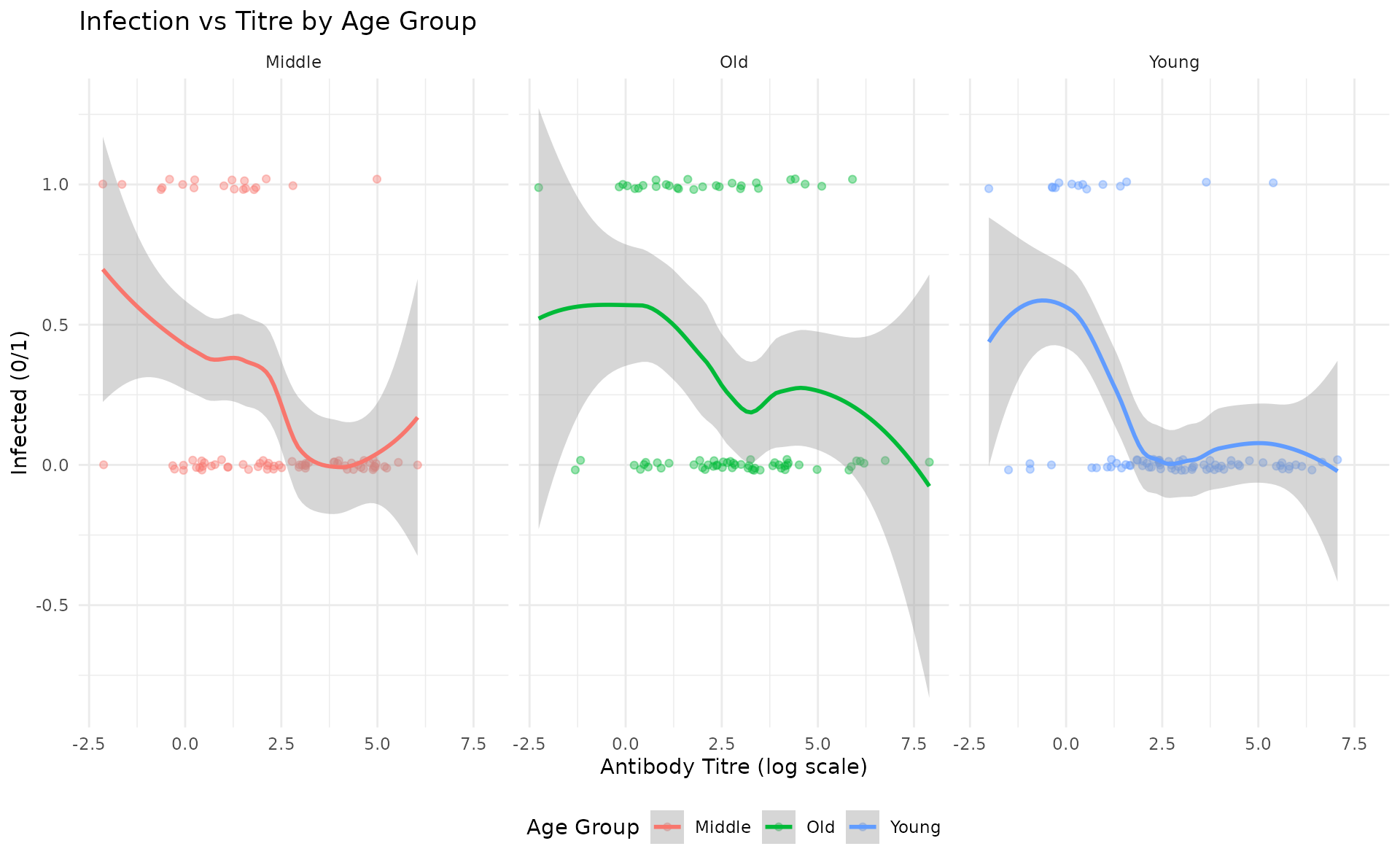

Fit Hierarchical Model

Now we’ll fit a hierarchical model that estimates group-specific slopes and EC50 values while sharing information across groups:

# Create SeroCOP object with group variable
hier_model <- SeroCOP$new(
  titre = all_data$titre,
  infected = all_data$infected,
  group = all_data$age_group  # Add group variable for hierarchical modeling
)

# Fit the hierarchical model
hier_model$fit_model(
  chains = 4,
  iter = 2000,
  warmup = 1000,
  cores = 4,
  refresh = 0
)
cat("✓ Hierarchical model fitted successfully!\n")
#> ✓ Hierarchical model fitted successfully!

Extract Group-Specific Parameters

The hierarchical model estimates both population-level parameters and group-specific deviations:

# Extract group-specific estimates
group_params <- hier_model$extract_group_parameters()
print(group_params)
#>    group parameter      mean    median        sd        q025     q975
#> 1 Middle      ec50 0.6655970 0.6314611 0.8188243 -0.93936907 2.222687
#> 2 Middle     slope 1.1869451 0.8854845 1.1705268  0.41918349 4.168349
#> 3    Old      ec50 1.1860790 1.1489617 1.2980409 -1.64254551 3.890460
#> 4    Old     slope 0.5365246 0.3958558 0.6187756  0.07937568 2.210292
#> 5  Young      ec50 0.6235339 0.7308970 0.6547243 -0.91529456 1.627658
#> 6  Young     slope 2.2283638 1.8292845 1.5514246  0.55463288 5.916504

The table shows:

  • ec50: The antibody level at which infection probability is 50% of maximum
  • slope: The steepness of the dose-response curve (higher = steeper)

Notice how: - Young group has the most negative (steepest) slope - Old group has a slope near zero (flat relationship) - Middle group is intermediate

Visualize Group-Specific Curves

We can plot the fitted curves for each group:

hier_model$plot_group_curves(title = "Age-Specific Correlates of Protection")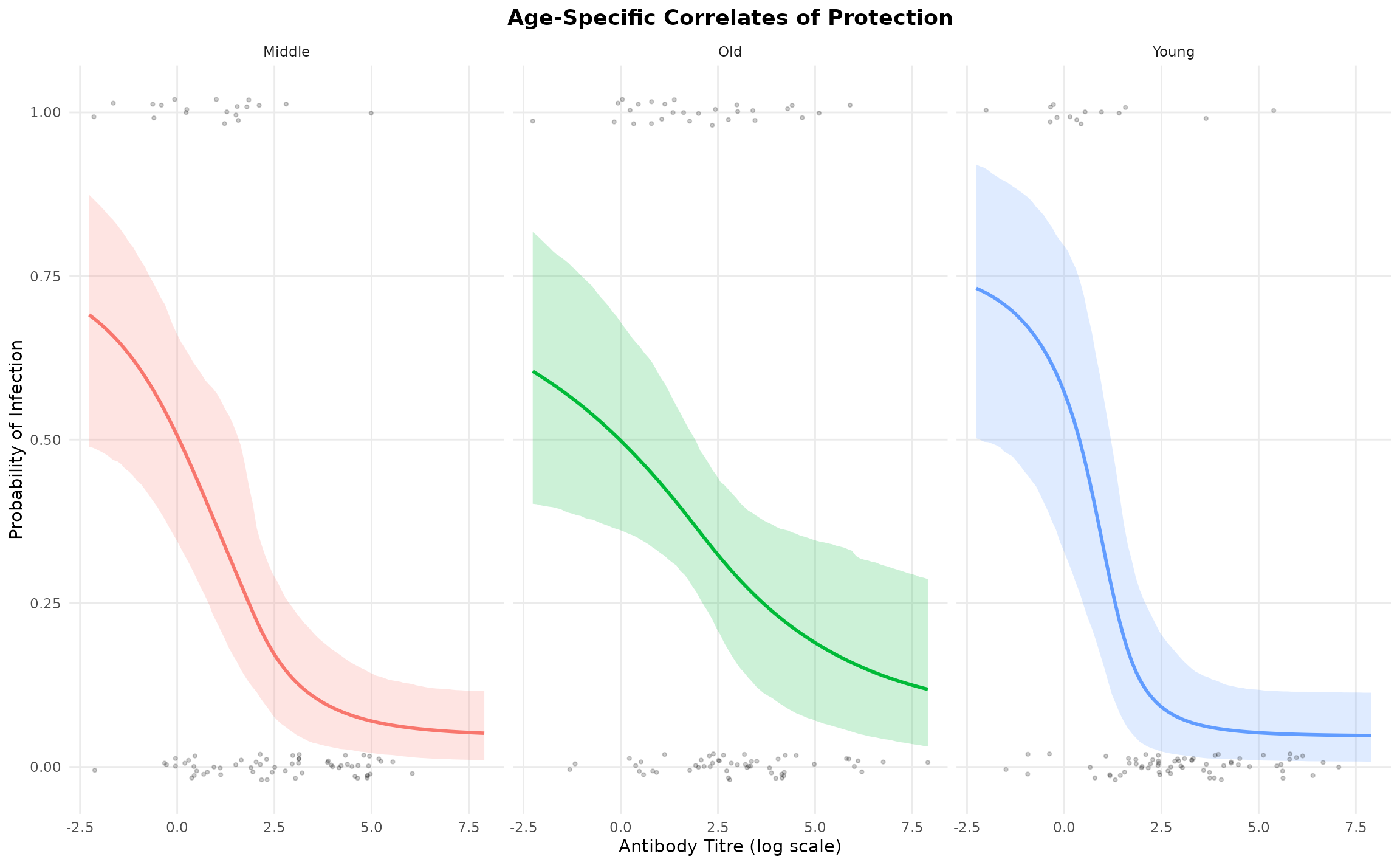

The plot shows:

  • Fitted curves (solid lines) for each age group
  • 95% credible intervals (shaded ribbons) reflecting uncertainty
  • Observed data points (dots) for each group
  • Clear differences in curve steepness across age groups

Compare with Non-Hierarchical Model

Let’s fit a standard (non-hierarchical) model that ignores age groups and see how it compares:

# Fit without group variable (pooled model)
pooled_model <- SeroCOP$new(
  titre = all_data$titre,
  infected = all_data$infected
)

pooled_model$fit_model(
  chains = 4,
  iter = 2000,
  warmup = 1000,
  cores = 4,
  refresh = 0
)
cat("✓ Non-hierarchical (pooled) model fitted successfully!\n")
#> ✓ Non-hierarchical (pooled) model fitted successfully!

Model Comparison

We can use Leave-One-Out Cross-Validation (LOO-CV) to compare model fit:

# Extract LOO estimates
hier_loo <- hier_model$loo$estimates["elpd_loo", c("Estimate", "SE")]
pooled_loo <- pooled_model$loo$estimates["elpd_loo", c("Estimate", "SE")]

# Calculate difference
loo_diff <- hier_loo["Estimate"] - pooled_loo["Estimate"]
loo_se <- sqrt(hier_loo["SE"]^2 + pooled_loo["SE"]^2)

cat("\n=== Model Comparison (LOO-CV) ===\n")
#> 
#> === Model Comparison (LOO-CV) ===
cat(sprintf("Hierarchical model ELPD: %.2f (SE: %.2f)\n", 
           hier_loo["Estimate"], hier_loo["SE"]))
#> Hierarchical model ELPD: -119.85 (SE: 8.37)
cat(sprintf("Pooled model ELPD:       %.2f (SE: %.2f)\n", 
           pooled_loo["Estimate"], pooled_loo["SE"]))
#> Pooled model ELPD:       -123.04 (SE: 8.24)
cat(sprintf("\nDifference: %.2f (SE: %.2f)\n", loo_diff, loo_se))
#> 
#> Difference: 3.19 (SE: 11.74)
cat(sprintf("Z-score: %.2f\n", loo_diff / loo_se))
#> Z-score: 0.27

if (loo_diff > 2 * loo_se) {
  cat("\n✓ Strong evidence favoring hierarchical model\n")
} else if (loo_diff > 0) {
  cat("\n→ Hierarchical model preferred but evidence is weak\n")
} else {
  cat("\n→ No clear advantage for hierarchical model\n")
}
#> 
#> → Hierarchical model preferred but evidence is weak

A positive difference indicates the hierarchical model fits better. The Z-score helps assess the strength of evidence (|Z| > 2 suggests strong evidence).

Visualize Both Models

Let’s compare the two approaches visually:

# For the pooled model, get predictions across the titre range
titre_grid <- seq(min(all_data$titre), max(all_data$titre), length.out = 100)
pooled_pred <- pooled_model$predict(newdata = titre_grid)
pooled_mean <- colMeans(pooled_pred)
pooled_lower <- apply(pooled_pred, 2, quantile, probs = 0.025)
pooled_upper <- apply(pooled_pred, 2, quantile, probs = 0.975)

# Create a simple comparison plot showing pooled model vs observed data by group
pooled_df <- data.frame(
  titre = titre_grid,
  prob = pooled_mean,
  lower = pooled_lower,
  upper = pooled_upper
)

ggplot() +
  geom_ribbon(data = pooled_df,
              aes(x = titre, ymin = lower, ymax = upper),
              fill = "gray", alpha = 0.3) +
  geom_line(data = pooled_df,
            aes(x = titre, y = prob),
            color = "gray30", linewidth = 1.2) +
  geom_point(data = all_data,
             aes(x = titre, y = infected, color = age_group),
             alpha = 0.4, size = 1.5,
             position = position_jitter(height = 0.02)) +
  geom_smooth(data = all_data,
              aes(x = titre, y = infected, color = age_group),
              method = "loess", se = FALSE, linewidth = 1) +
  facet_wrap(~age_group) +
  labs(
    title = "Pooled Model vs Age-Specific Data",
    subtitle = "Gray line = pooled model (same for all groups); Colored lines = observed LOESS fits",
    x = "Antibody Titre (log scale)",
    y = "Probability of Infection",
    color = "Age Group"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")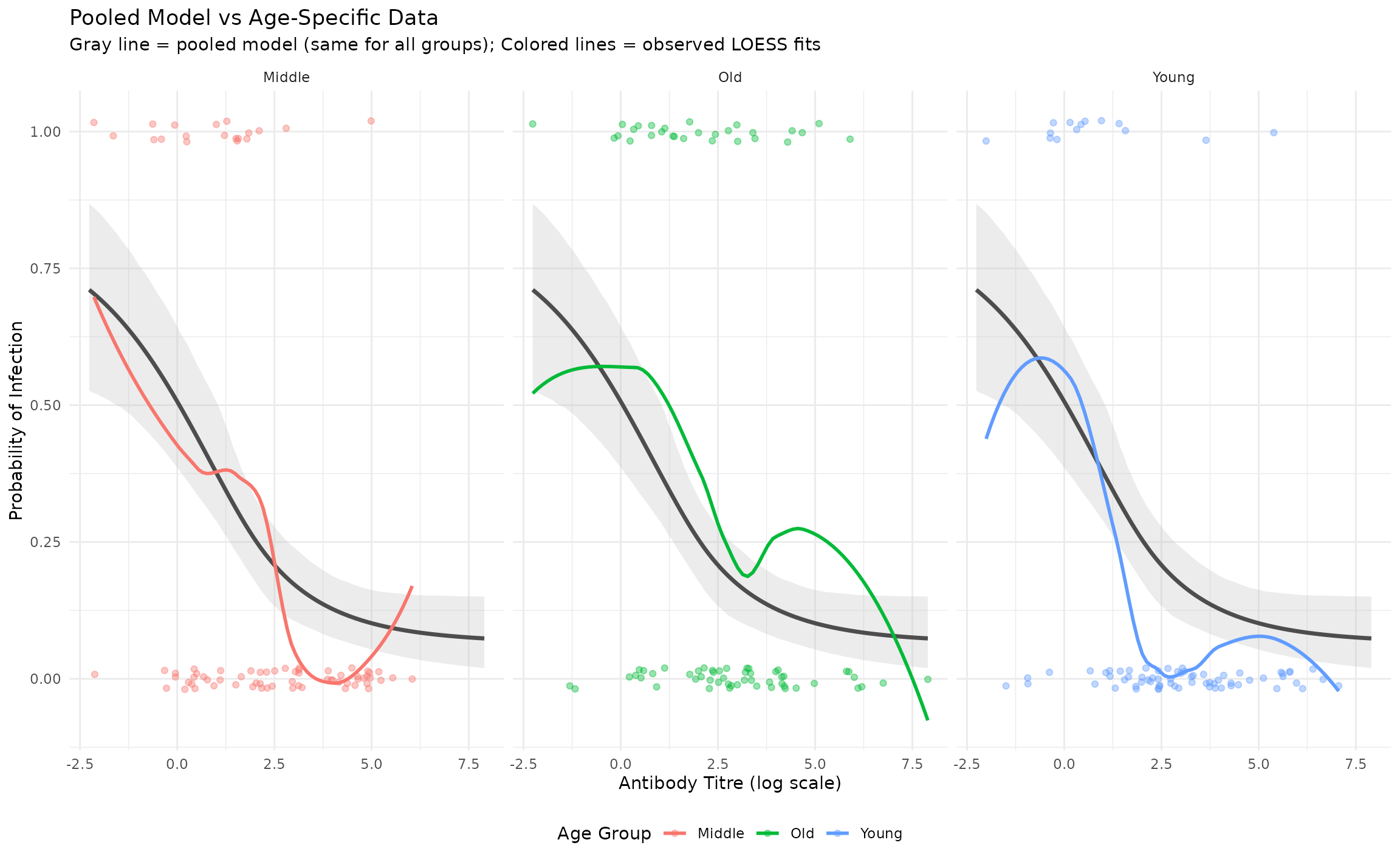

Note how: - The pooled model (gray line) uses the same curve for all age groups, ignoring heterogeneity - The observed patterns (colored LOESS curves) show clear age-specific differences - The hierarchical model (shown in the previous plot) captures these group-specific relationships - The pooled approach misses important variation, particularly the flat relationship in older adults

Key Advantages of Hierarchical Modeling

  1. Partial Pooling: Groups share information, improving estimates for small groups
  2. Heterogeneity: Captures real differences between groups
  3. Better Predictions: More accurate for group-specific outcomes
  4. Quantifies Variability: Estimates between-group variance in parameters

Technical Details

Model Structure

The hierarchical model uses random intercepts on the ec50 and slope parameters:

ec50 ~ 1 + (1 | group)
slope ~ 1 + (1 | group)

This means: - Each group gets its own ec50 and slope value - Group-specific values are drawn from a common distribution - The model estimates both the population mean and group-level variance

Priors

The model uses weakly informative priors: - Group-level standard deviations: student_t(3, 0, 2.5) - This allows substantial between-group variation while regularizing extreme values

Backwards Compatibility

To fit a standard (non-hierarchical) model, simply omit the group parameter:

# Non-hierarchical
model <- SeroCOP$new(titre = titre, infected = infected)

# Hierarchical
model <- SeroCOP$new(titre = titre, infected = infected, group = age_group)

Conclusion

Hierarchical modeling in SeroCOP provides a powerful framework for analyzing correlates of protection when you expect heterogeneity across groups. The approach:

  • Provides group-specific estimates while sharing information
  • Improves model fit and predictive accuracy
  • Quantifies between-group variability
  • Is easy to implement with the optional group parameter

This is particularly valuable in real-world scenarios where immune responses vary by demographics, vaccine types, or other grouping factors.

Session Info 

sessionInfo()
#> R version 4.5.2 (2025-10-31)
#> Platform: x86_64-pc-linux-gnu
#> Running under: Ubuntu 24.04.3 LTS
#> 
#> Matrix products: default
#> BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
#> LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0
#> 
#> locale:
#>  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
#>  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
#>  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
#> [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
#> 
#> time zone: UTC
#> tzcode source: system (glibc)
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#> [1] ggplot2_4.0.1 seroCOP_0.1.0
#> 
#> loaded via a namespace (and not attached):
#>  [1] gtable_0.3.6          tensorA_0.36.2.1      xfun_0.54            
#>  [4] bslib_0.9.0           QuickJSR_1.8.1        processx_3.8.6       
#>  [7] inline_0.3.21         lattice_0.22-7        callr_3.7.6          
#> [10] ps_1.9.1              vctrs_0.6.5           tools_4.5.2          
#> [13] generics_0.1.4        stats4_4.5.2          parallel_4.5.2       
#> [16] tibble_3.3.0          pkgconfig_2.0.3       brms_2.23.0          
#> [19] Matrix_1.7-4          checkmate_2.3.3       RColorBrewer_1.1-3   
#> [22] S7_0.2.1              desc_1.4.3            distributional_0.5.0 
#> [25] RcppParallel_5.1.11-1 lifecycle_1.0.4       compiler_4.5.2       
#> [28] farver_2.1.2          stringr_1.6.0         textshaping_1.0.4    
#> [31] Brobdingnag_1.2-9     codetools_0.2-20      htmltools_0.5.8.1    
#> [34] sass_0.4.10           bayesplot_1.14.0      yaml_2.3.11          
#> [37] pillar_1.11.1         pkgdown_2.2.0         jquerylib_0.1.4      
#> [40] cachem_1.1.0          StanHeaders_2.32.10   bridgesampling_1.2-1 
#> [43] abind_1.4-8           nlme_3.1-168          posterior_1.6.1      
#> [46] rstan_2.32.7          tidyselect_1.2.1      digest_0.6.39        
#> [49] mvtnorm_1.3-3         stringi_1.8.7         dplyr_1.1.4          
#> [52] labeling_0.4.3        splines_4.5.2         fastmap_1.2.0        
#> [55] grid_4.5.2            cli_3.6.5             magrittr_2.0.4       
#> [58] loo_2.8.0             pkgbuild_1.4.8        withr_3.0.2          
#> [61] scales_1.4.0          backports_1.5.0       rmarkdown_2.30       
#> [64] matrixStats_1.5.0     gridExtra_2.3         ragg_1.5.0           
#> [67] coda_0.19-4.1         evaluate_1.0.5        knitr_1.50           
#> [70] mgcv_1.9-3            rstantools_2.5.0      rlang_1.1.6          
#> [73] Rcpp_1.1.0            glue_1.8.0            jsonlite_2.0.0       
#> [76] R6_2.6.1              systemfonts_1.3.1     fs_1.6.6